And thinking some more about Caitlin's observation:
Consider that -1 = Exp[Pi I], then an nth root of -1 is Exp[Pi I / n].
The north nth roots of unity are given by Exp[2 Pi I k / northward] with chiliad from 1 to n. (de Moivres numbers)
Multiplying the nth root of -1 by these gives the due north nth roots of -1 every bit Exp[(2k+1) Pi I / n], again with k from 1 to n.
Since any negative number -Due north (N positive) tin can be written as -one*Northward, we have the nth root as the master root of Due north multiplied by these n roots of -1.
Hither, for example, are nine ninth roots of -i:
In[one]:= rootOfMinusOne[k_, n_] := Exp[(ii grand + 1) Pi I/due north] In[2]:= roots9 = Table[rootOfMinusOne[k, 9], {thousand, 9}] Out[2]= {East^((I \[Pi])/3), Due east^((5 I \[Pi])/nine), E^(( 7 I \[Pi])/ix), -i, E^(-((7 I \[Pi])/9)), E^(-((5 I \[Pi])/9)), Eastward^(-(( I \[Pi])/iii)), E^(-((I \[Pi])/9)), E^((I \[Pi])/9)} In[3]:= #^nine & /@ roots9 Out[3]= {-1, -i, -1, -1, -1, -1, -1, -1, -1} In[iv]:= cPlot[lst_, opts___] := ListPlot[{Re[#], Im[#]} & /@ lst, AspectRatio -> one, AxesLabel -> {"Re", "Im"}, opts] In[five]:= cplt = cPlot[roots9, PlotLabel -> "The 9 ninth roots of -1"] 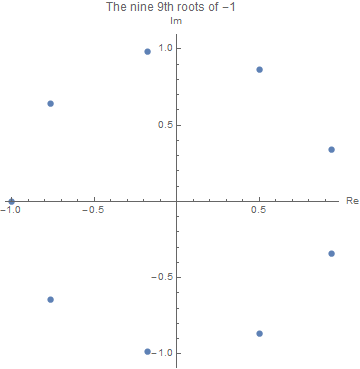
0 Response to "Wolfram Mathematica How to Make X Become X Again"
ارسال یک نظر